Statistics 101 for aspiring data scientists – Lesson 1

In truth, every human can be loosely held to be a data scientist, at a very micro level.
From time immemorial, human beings have collected, analysed, and used information for the gamut of human endeavours. We thrive on data. We collect it even without trying. It is built into our biology. Take, for instance, all the ways in which we know when someone’s lying. That’s our body and mind collecting information about the other person’s verbal and non-verbal cues, analysing them, and reaching a conclusion.
With the evolution of IT and now Big Data, data science has evolved as a field that is not simply important today but vital to our futures as well. And data science courses help aspirants collect, bifurcate, analyse, and understand reams and reams of data – at a macro level.
To go from understanding data at cellular level to a global level, you need to undertake a data science course, and before that, you need to gain a firm grasp of key Statistics concepts. Anticipating this,
Eruditus has compiled a comprehensive yet slim e-book, Statistics for Data Science, containing concepts that are essential to your data analytics course as well as your career. Even before you’re on your way to data science certification, we make sure that you are able to peer into the data abyss, and see light.
Our handy ebook is helpful for not just online data science courses but also machine learning courses, artificial intelligence courses, machine learning applications, and more. However, we also recognise that due to factors like time or just plain convenience, you might like to absorb Statistics concepts online too.
We’re happy to present a new series of ten blog posts: Statistics 101 for Data Science! Drawn from our in-depth ebook, these blogs will present key statistical concepts in a truncated form, for your convenience.
In this article, you will get the answers to the following questions:
- What is probability?
- How probability is relevant to data science
- What is joint probability?
- What is conditional probability?
- What is marginal probability?
- Take a quiz to test yourself and find out what python code to use in these concepts
Let’s get started with our first concept: Probability.
What is probability?
Certain events or outcomes, like the rising of the sun, are more likely than, say, rolling a certain number on the dice at any time. A coin, when tossed, can only land on heads or tails aka two outcomes – making the probability of either equal or 50-50.
Let’s use the coin example to understand this better. When you toss a coin, you can have only two possibilities or outcomes. You also have one desired outcome – either heads or tails. Thus, the chance of heads or tail tails in a coin toss is the same 0.5.
Probability is the statistical term that replaces chance and possibility in these contexts. Probability quantifies the likelihood of an event for a random variable. In this example, the flip of the coin is the random variable. It is a variable because the values can change, and it is random because we can’t control the outcome. The total number of outcomes that can happen is referred to as the Sample Space.
A probability of 0 means that the desired outcome is impossible. In a coin toss, you can never have both heads and tails show up at the same time, unless of course, you’re cheating.
How is probability relevant to data science training, machine learning or AI courses?
Given a set of random variables, you can calculate sample space and probability of likely outcomes. This is at the very heart of data science, AI, and machine learning – disciplines that use huge volumes of past data to predict the future. Data scientists utilise these disciplines to solve problems across business, humanity, healthcare, and more.
The applications are immense:
- Predict future sales and customer churn through historical data
- Learn from past images to identify new unknown images
- Use past customer purchase data to predict and recommend new products
- Use past credit history to predict which customers will default
You will always rely on historical data – which is always imperfect and uncertain. This is due to measurement errors and gaps in data capture. The future is not certain, but one can make probabilistic predictions about possible outcomes.
However, real life has multiple random variables, interacting with each other – unlike a coin toss. So to navigate the many permutations and combinations, you need tools like joint, conditional, and independent probability.
What is joint probability?
It describes the probability of the outcomes of two simultaneously occurring random variables.
Let’s say the following table represents the top 3 shows on TV streaming service Netstar and the demographic breakdown of the number of viewers.
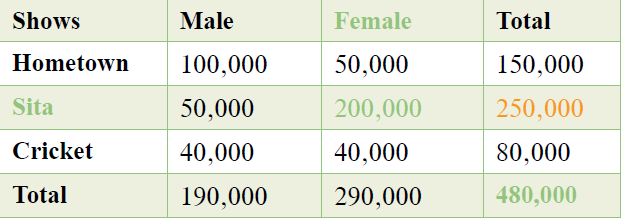
What is the probability of a female viewer watching the show Sita?
There are two levels of probability here – first, that the viewer is female and second, that this female viewer watches Sita.
P (Female and Sita)
= Number desired outcomes (200,000) / Total number of outcomes (480,000) = 0.42
Assuming random variable A represents female viewers and random variable B represents Sita, calculating the joint probability using the formula would give us the same answer:
P (A and B) = P (A | B) x P (B) = (200,000 / 250,000 = 0.8) x (250,000 / 480,000 = 0.52) = 0.42
The applications of joint probability are wide-ranging.
As you can see, entertainment streaming companies gain insights on what segment of viewers like what shows, through data science, to allocate the right budgets for new shows and for marketing activities.
Supply chain and logistics companies can also use data science to predict congestion of traffic. Assume hubs A and B have trucks coming in and leaving. Through joint probability, you can predict the number of trucks coming into Hub A during a particular time duration T, and trucks leaving Hub A in the same time duration.
What is conditional probability?
This is the likelihood that an event will occur given the knowledge that another event has already occurred.
Let’s continue using the above example.
If a viewer, Reena, just got a Netstar subscription, what is the probability that her favorite show will be Hometown?
Now, you have already been told about a condition – that the viewer, Reena, is female. To estimate the probability of one random variable A (her favorite show being Hometown), having been given a conditional random variable B (female Netstar subscriber), is what conditional probability is all about.
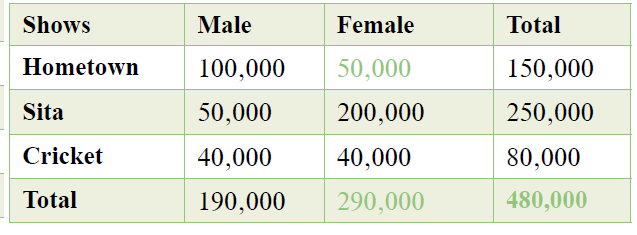
Expressed as a formula:
P (A|B) = P(A and B) / P(B) = (50,000 / 480,000 = 0.1 ) / (290,000 / 480,000 = 0.6) = 0.17
There is a 0.17 probability that Reena will watch Hometown. The given conditions in this problem is that Reena is female.
The applications of conditional probability are quite vast.
It is typically used when time series data (data points collected at successive time intervals) is involved or in the case of events occurring on a particular day, depending on developments of previous days e.g., share prices, weather forecasts, etc.
For example, the weatherman might estimate a probability of rain of 40 percent, which is conditional upon the probability of many factors such as:
- a cold front coming to the area
- the formation of rain clouds
- another front pushing rain clouds away
What is marginal probability?
This is the probability of an event for a random variable irrespective of the outcome of other random variables.
Continuing the Netstar example, what if we had to find a) the probability of a Netstar viewer watching Hometown and b) the probability of a Netstar viewer being male?
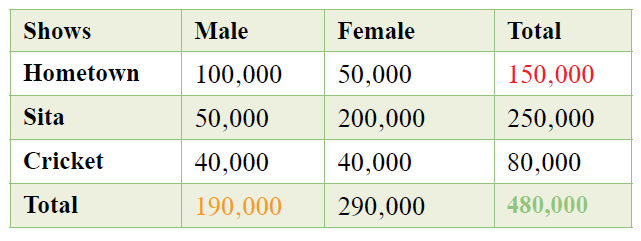
0.31 (150,000/480,000) is the probability that a Netstar viewer watches Hometown.
0.39 (190,000/480,000) is the probability that a Netstar viewer is male.
Can I take a quiz? Can we use python code to implement these concepts?
Yes, you absolutely can do both with the free to download Statistics for Data Science ebook, which offers those codes in detail, as well as the relevant formulae for these concepts, and a handy quiz as well.
Can we explore data science courses to learn more?
Eruditus offers a range of data science courses from IIM Kozhikode, IIM Lucknow, IIT Delhi, IIT Bombay, and more.

